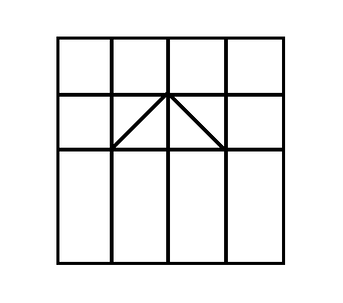
Part one...One Part AmazingDay 106My day was really like two separate days. One part was amazing and the other heartbreaking. We should definitely start with the amazing. We wrapped up a unit in math and it was Friday. I felt like we should have some fun. We started our day with a fraction talk. (www.fractiontalks.com) I love the geometric images there. The partitioning of these images help kids to make meaning of fractions. The images allow my students to reason about relative size and they help to build understanding around equivalency. Plus, kids like them. There is a puzzle-like nature to them that makes them seem fun. Today was the first day my students experienced a fraction talk. One of the images we used was the image below: We used the #noticeandwonder routine to start our conversation. The students made some rich observations. Given that the "whole" is the large square, they noticed that the square had been decomposed into squares, rectangles and triangles. They noticed that the second row would be identical to the first if not for the two squares that were decomposed into triangles. They wondered how many squares it would take to cover the whole. They wondered the same thing about the triangles and the rectangles. They were able to visually partition the shape to figure out the fraction value of each shape. This lead them to more wondering. If the value of one small square is 1/16 the whole, what is the value of the top row? What about the value of the first column? How many different ways can you visually represent the sum of parts equal to one fourth. (eg: rectangle plus rectangle - 1/8 + 1/8 or two small squares plus four triangles - 1/16 + 1/16 + 1/32 + 1/32 + 1/32 + 1/32) The images really do engage my students. It was exciting for me to see them make meaning of fractions. It made me happy to begin learning about fractions in this way. I love this resource. Then, because it was Friday, and Fridays should be fun, we culminated our unit on multiplication with a 3-Act Task by @gfletchy ( https://gfletchy.com/ ) If you haven't explored Graham Fletcher's site yet, now is the time. We used a task today titled, "Piles of Tiles". While Graham has it lumped in with the third grade tasks as it addresses 3.MD.5,6.7, it is great place for fourth graders to begin when they're first being introduced to these tasks. Even though fourth graders should be able to multiply using powers of ten and should be able to compute area by decomposing a whole into parts, this task is always super challenging for them. The first act in this task is the watching of a very short video. In the video they see a man (Graham) sit down at a table shaped like a giant "plus" sign. He has a gigantic bag of square tiles. He begins to lay the tiles on the table. The students begin to #noticeandwonder. In the end, they are asked to estimate how many tiles are in the bag. They are encouraged to make brave estimates. The estimate a number that is too small but still brave. (ten or even 100 would not be considered a brave estimate.) Many of my students estimated 1,000. Then they estimated a number that was too large but still fairly brave. Estimates ranged from 3,000 to 5,000. They they were asked to estimate using a estimate as exact as possible. While the estimates still ran the gamut, they were all in a reasonable range. The question became: "will there be enough tiles to cover the table?" They were asked what further information they'd like to have access too. This is where my students fell short. They should have had enough experience with square tiles to know that they are one square inch in size. I wish they had wanted to know the size of the table. Instead, they asked how many square tiles it would take to cover the whole table. Some wanted to know how many tiles were in the bag. Hopefully, with more exposure to tasks like this that require deep thinking they will get better at thinking like a mathematician and will have an easier time engaging with a challenging task. The second act revealed some helpful information. The students examined the below images. I was surprised at how hard a time they had making sense of the table diagram. As they set off to work, I was surprised by how many students wanted to just "number grab" and solve without making sense first. Some wanted to add 60 and 60 and say that it would take 120 tiles to cover the table! They weren't at all concerned with the 1,842 tiles in the bag and didn't stop to consider how ridiculous the question was if it only took 120 tiles to cover the table. I had to prompt them to really consider what the red arrows were telling them. Once they could make meaning of the diagram, they were fairly successful in determining that the length of a short side had to be twenty. I did have to ask some groups to decompose the table into smaller sections and to name the shape of the sections they created. Some teams who said that one side was equal to twenty square tiles wanted to say that the other short side was equal to ten. They saw the arrow bisecting the shape and allowed themselves to think that they needed to "cut" the twenty in half. Even after some teams were able to label their diagrams such that they had five squares with sides of 20, they wanted to say that it took 40 or 80 tiles to cover the smaller squares. It was clear to me that even though these kids probably could have spouted off the formula for area, they had little idea of how this knowledge could be applied to problem solving. Over the course of the lesson, I walked from group to group asking "why?" "What makes you think so?' "So, what does that make you wonder?" etc. It is hard not to ask leading questions. It is hard not to give hints. It is REALLY hard to prevent the other adults from becoming teaching members of each group! As teachers, we have to fight the instinct to over-help and give "hints". It takes power away from our students. In the end, after a lot of perseverance and struggle, every team was able to arrive at a solution that worked. Some got there in very round-about ways, but they got there. When we debriefed and viewed the final act, the kids were in consensus. The work had been REALLY satisfying. What I noticed was that every group worked effectively. No one was left behind. Of course, some students contributed more. Some were leaders and some did their best to merely follow the thinking of their peers. Regardless, this was an enormously successful first dive into a 3-Act Task.
It had been a purely amazing mathematical morning. And then...read the post for Day 106 to find our how our day ended with a heartbreaking twist.
0 Comments
Leave a Reply. |
Marie McManus BrighamA public school teacher who gets to wonder alongside fourth-graders. Archives
December 2018
Categories |


 RSS Feed
RSS Feed